examples of 3d faces drawings facing forward

i. Introduction

3D face has been extensively applied in the areas of face recognition (Artificial and Aryananda, 2002; Mian et al., 2006), expression recognition (Zhang et al., 2015). These confront analysis technologies are of significance for homo-robot cooperative tasks in a rubber and intelligent land (Maejima et al., 2012). So 3D face reconstruction is a import topic, and it is meaningful to reconstruct specific 3D face from person-of-interest images under many claiming scenes. The images under challenge scene are also referred as images in the wild, having following characteristics: (1) significant changes in illuminations across time periods; (two) diverse confront poses caused by different camera sensors and view points; (3) different appearances among different environs; (four) occlusions or redundant backgrounds. More seriously, only limited number of identity images are bachelor under human-robot interaction, surveillance, and mobile shooting scenario as listed in Figure 1, sometimes.

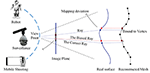
Figure 1. Geometric optics of BP (i.e., back projection) imaging on two types of surfaces: the correct ray lines become through the bluish points on the truthful shape, while the biased ones become through blood-red points on the mesh shape considering the cantankerous betoken betwixt a ray and mesh is bounded to vertex. The difference between red point and the bluish point is referred to local mapping departure.

As a whole, reconstruction technologies include single-image method, multiple images, and even unconstrained images based methods. Recent researches (Kemelmacher and Seitz, 2011; Roth et al., 2015, 2016) testify that good reconstruction depends on two aspects of efforts: (1) enough rich local information, east.thousand., normal, and (2) a good face prior, eastward.g., face template. Particularly, the latter is to find an embedding representation with good feature to register local data finely.

According to the template representation, these methods tin can be categorized into three classes: (i) methods without using template, due east.g., integration (Kemelmacher and Seitz, 2011) and structure from movement (Koo and Lam, 2008), (ii) methods using a single discrete template, e.g., a reference confront mesh (Roth et al., 2015), and (iii) methods using a statistic continuous template, e.1000, T-splineMMs (Peng et al., 2017), or discrete template, due east.g., 3DMMs (Piotraschke and Blanz, 2016; Roth et al., 2016). The methods with template always generate good global shape compared with those without template, and a statistic template contributes to a meliorate personalization. Therefore, it is very significant to find a excellent template representation for face up reconstruction. Mesh model is widely used due to its rapid ciphering and popularity in computer vision, simply it is non well-compatible with geometric optics in vertex level, resulting in local mapping departure of rays, seen in Figure 1. This makes local information not strictly registered physically. Additional, discretization of Laplace-Beltrami functioning (LBO), i.due east., cotangent scheme (Meyer et al., 2003), may bring a deformation distortion at local, which frequently happens when images are non plenty for high-quality normal estimation. This baloney irregularly occurs at the edge and the location with large curvature irresolute, e.thousand., nose and rima oris. Lastly the topology-fixed mesh besides restricts an extended refinement. All in a higher place trouble limits reconstruction precision of mesh.

To solve the existing consequence in mesh template, nosotros adopt classic B-spline embedding office (Piegl and Tiller, 1997) to register local information and reconstruct face. Firstly, B-spline surface is a parametric surface that can estimate the true shape of an object with fewer parameters (control points) than mesh. It contributes to correct rays in geometric optics, that makes local data, i.e., texture, feature points and normals, accurately registered. Secondly, we utilise 2nd-lodge partial derivative operator w.r.t. parameters as the local deformation constraint to reduce the deformation distortion. Lastly, B-spline surface also can be used to generate mesh in whatsoever precision or be extended for farther refinement. The three characteristics of B-spline face show slap-up advantages over a mesh template based method. Given a collection of images, we use B-spline embedding office as 3D face representation and model 0th- and 1st-order consistency of reconstruction in the parameter domain, which makes BP imaging rays completely uniform with geometric optics. The 0th-order consistency model guarantees that the images are well-registered to surface fifty-fifty if the face up images has occlusion or expression; And the 1st-lodge consistency model guarantees that the surface normals is consistent to the normals estimated from images. Both qualitative and quantitative experiments are conducted and compared with other methods.

In a nutshell, in that location are two primary contributions:

1. Pinpoint geometrical consistency is modeled on B-spline embedding function for face reconstruction from multiple images, completely consequent with the law of geometric eyes.

2. 0th- and 1st-society consistency weather condition and its a practical solution is proposed to optimize B-spline face finer, which is able to handle variations such as different poses, illuminations, and expressions with limited of number images.

In the post-obit, we will get-go review related work in department two. Section 3 provides a geometric modeling of multiple BP imaging in prototype-based stereo for our problem. Nosotros innovate the B-spline embedding and its brief representations in section 4 and present consistency modeling for B-spline face reconstruction in section 5. In addition, a practical solution is proposed in section six. We conduct experiment in section 7 and conclude in section 9.

2. Related Work

2.ane. 3D Face Required Scenes

With the evolution of robots and AIoT (Qiu et al., 2020), vision volition play an very important office in safety (Khraisat et al., 2019; Li et al., 2019), scene and human understanding (Zhang et al., 2015; Meng et al., 2020). As a base of operations technology, 3D face up contributes to the scenes profoundly. For example, to build humanoid robots that interact in a homo-understanding fashion, automatic face, and expression recognition is very import (Zhang et al., 2015). The recognition during real-life man robot interaction could still exist challenging as a result of discipline variations, illumination changes, diverse pose, background clutter, and occlusions (Mian et al., 2006). All the same, humanoid robot API of original version cannot e'er exist able to handling such challenges. Optimal, robust, and accurate automated face analysis is thus meaningful for the real-life applications since the performance of facial action and emotion recognition relies heavily on it. Many parametric approaches like 3DMMs (Blanz and Vetter, 1999; Blanz et al., 2004) and face alignment with 3D solution (Zhu et al., 2016) in the computer vision field have been proposed to estimate caput pose, recognition identity, and expression from real-life images to benefit subsequent automated facial behavior perception to address the above problems. Therefore, 3d face modeling in a humanoid robot view is of great significant to handling the challenging face up analysis during interaction.

2.2. 2d Images Based Face Reconstruction

2D methods generally cover several kinds of key methods including Structure from Move (SFM) (Tomasi and Kanade, 1992), Shape from Shading (SFM) (Zhang et al., 1999), 3D Morphable Model (3DMM) (Blanz and Vetter, 1999; Blanz et al., 2004), and Deep learnings (Richardson et al., 2017; Deng et al., 2019). SFM methods compute the positions of surface points based on an assumption that there exists a coordinate transformation betwixt the image coordinate organization and the camera coordinate system. And SFS methods compute surface normals with an assumption that the subject surface is of Lambertian and under a relatively afar illumination. And the thought of 3DMM is that human faces are within a linear subspace, and that whatever novel face up shape tin be represented by a linear combination of shape eigenvectors deduced by PCA. SFS and SFM give the geometrical and physical descriptions of confront shape and imaging, and 3DMM concentrates on the statistical explanation of 3D meshes or skeletons. Deep learning methods infer 3D face shape or texture (Lin et al., 2020) by statistically learning mapping betwixt face images and their 3D shapes (Zhou et al., 2019). Being limited to data size, most of them relies 3DMM or PCA for synthesizing supplementary ground truths (Richardson et al., 2016) or every bit a priori (Tran et al., 2017; Gecer et al., 2019; Wu et al., 2019), resulting absenteeism of shape detail. It's believed that face reconstruction is rather a geometrical optimization problem than a statistical problem, every bit 3DMM is more suitable to exist an assistant of the geometrical method when building detailed shape, eastward.g., that by Yang et al. (2014).

2.iii. Shape in Shading and Structure in Motion

SFS has been widely used for reconstruction, due east.grand., single-view reconstruction (Kemelmacher Shlizerman and Basri, 2011), multiple frontal images based reconstruction (Wang et al., 2003), and unconstrained image based reconstruction (Kemelmacher and Seitz, 2011; Roth et al., 2015). As single-view is ill posed (Prados and Faugeras, 2005), a reference is always needed (Kemelmacher Shlizerman and Basri, 2011). For unconstrained images, photometric stereo is applied to obtain accurate normals locally (Kemelmacher and Seitz, 2011; Roth et al., 2015). SFM uses multiple frame or images to recover sparse 3D construction of feature points of an object (Tomasi and Kanade, 1992). Spatial-transformation arroyo (Sun et al., 2013) just estimates the depth of facial points. Bundle adjustment (Agarwal et al., 2011) fits the large scale rigid object reconstruction, but it cannot generate the dense model of not-rigid face. Incremental SFM (Gonzalez-Mora et al., 2010) is proposed to build a generic 3D face model for non-rigid face. The piece of work by Roth et al. (2015) optimizes the local information with normals from shading, based on a 3D feature points-driven global warping. Therefore, shading and motion are important and very distinct geometric information of face, and they enhance the reconstruction when being combined. In our method, 0th- and 1st-society consistency of stereo is modeled to integrate the advantages of both shading and motion data.

2.4. Facial Surface Modeling

Surface modeling is dependent on the information input (point cloud, noise, outlier, etc), output (point deject, mesh, skeleton), and types of shape (human being-fabricated shape, organic shape). Bespeak deject, skeleton, and mesh grid are the widely used man-made shape type for face reconstruction. Lu et al. (2016) nowadays an a stepwise tracking method approach to reconstruct 3D B-spline space curves from planar orthogonal views through minimizing the energy function with weight values. Spatial transformation method (Dominicus et al., 2013) estimates positions of sparse facial feature points. Package adjustment builds the dumbo point deject for large scale rigid object with a swell number of images (Agarwal et al., 2011). Heo and Savvides (2009) reconstruct confront dense mesh based on skeleton and 3DMM. Kemelmacher and Seitz (2011) utilise integration of normals to become detached surface points, which may produce incredible depth when the recovered normals are unreliable. Roth et al. (2015) reconstruct face up mesh based on Laplace mesh editing, which may produce local mesh distortion after several iterations of local optimization. In piece of work of mesh reconstruction, surface-smoothness priors is likewise needed to guarantee the smoothness of discrete mesh based on point cloud, e.g., radial basis office (Carr et al., 2001) and Poisson surface reconstruction (Kazhdan et al., 2006). Due to the fact that the point cloud and 3D mesh are discontinuous geometric shape, they cannot approximate the true shape of a face of arbitrary precision. There have been works of plumbing equipment B-splines to noisy 3D data, like Hoch et al. (1998). B-spline face model is a continuous costless-form surface that can be reconstructed from images directly, instead of intermediate point data, only it is not a detailed model by only using structure optimization (Peng et al., 2016). Because B-spline surface is a special case of NURBS (Non-Uniform Rational B-Spline) (Piegl and Tiller, 1997), it tin can also exist imported to 3D modeling software like Rhino3D for further editing, assay, and transformation conveniently by adjusting the B-spline control points. Information technology tin can too be converted into mesh model with any precision according to appropriate parameter interval, conveniently, which is meaningful for a arrangement with limited memory.

3. Geometric Modeling

Our problem modeling is illustrated in Figure 2. The domain of input image I _i from a camera is ${{I}}_i\subset {ℝ}^{\mathrm{two}},i=\mathrm{i},2,\dots ,n$. Π⁻¹ denotes the inverse operator of Π. The camera operator ${\Pi }_i\in C^{\infty }({ℝ}^{\mathrm{iii}},{ℝ}^{\mathrm{two}})$ map a point $P\in {Southward}$ to $p={\Pi }_i(P)\in {{I}}_i$ using weak perspective projection, i = 1, 2, …, n. And ${\Pi }_i^{-1}$ determines the ray cluster Rays#i of BP imaging from ${{I}}_i,i=1,2,\dots ,n$. Allow south _i , R _i , and t _i denote calibration, rotation, and translation parameter in projection Π _i . The ithursday projection operation is simply

$\begin{array}{ll}{\Pi }_i(P)\triangleq s_i·R_{i,\left[1,2\right]}·P+t_i.& (1)\end{array}$

R _{i, [1,2]} expresses the first two rows of R _i .

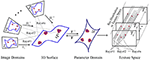
Figure 2. Geometric optics of multiple BP imaging.

Let ${U}\subset {ℝ}^{\mathrm{ii}}$ denote the parameter domain of homo face surface. A certain embedding $\text{F}\in C^{\mathrm{ane}}({U},{ℝ}^{\mathrm{iii}})$ maps a point $\text{u}\in {U}$ to the 3D point $P\in {S}$. F ⁻¹ denote the inverse operator of F. It is thus clear that unlike embedding F determine different face shapes. According to the geometric eyes of BP imaging, a image indicate $p\in {{I}}_i$ is back projected onto a point $\text{u}={\tau }_i(p)\in {U}$ via the operator

Therefore, an image I _i in the i-thursday view is mapped to surface S, and and so is mapped to texture space by

where we ascertain

$\begin{array}{ll}(I◦{\tau }^{-1})(\text{u})\triangleq I(\Pi (\text{F}(\text{u}))),for\text{u}\in {U}.& (4)\end{array}$

In fact, τ _i , i = 1, 2, …, n generate detached and inconsistent rays mapping in texture space because of the discrete and different images domains, too as the noises, seen in Figure 2.

three.1. 0th- and 1st-Gild Consistency

By and large, the problem is how to determine F according to from multiple images. If all images are the captures of a same ${Southward}$, all ${\left\{{{T}}_i\right\}}_{i=1:n}$ in texture space are hoped to exist highly consequent in the geometry.

First, that satisfies

$\begin{array}{ll}<\widehat{\text{F}},\left\{{\widehat{\Pi }}_i\right\}>=\underset{\text{F},\left\{{\Pi }_i\right\}}{\text{arg}\text{ min}}\text{ rank}(\left[\text{vec}({{T}}_1),\text{vec}({{T}}_2),\dots ,\text{vec}({{T}}_{\mathrm{northward}})\right]),& (5)\end{array}$

with ${{T}}_i={(I_i◦{\tau }_i^{-1})}^{\#},i=\mathrm{ane},2,\dots ,n$. And (·)^# is a composition operator of fitting and sampling, to handle the inconsistency. It firstly fits a texture role based on the discrete texture and parameters mapped from ane image, and then samples texture intensity values at unified parameter points {u _j } _{j=1 : N p} .

2d, information technology satisfies

$\begin{array}{ll}\{\begin{array}{l}\frac{\frac{\partial \text{F}}{\partial u}\times \frac{\partial \text{F}}{\partial 5}}{\left|\right|\frac{\partial \text{F}}{\partial u}\times \frac{\partial \text{F}}{\partial \mathrm{five}}\left|\right|}=n,\\ {\rho }_j{n}_j·l_i={{T}}_i{|}_{{\text{u}}_j}.\end{array}& (6)\end{array}$

which describes the equivalence relation between normal north and 1st-club fractional derivative in the first formulation, and the equivalence relation among albedo ρ, normal north , lite direction fifty , and image intensity ${T}$ in the 2nd. This follows a linear photometric model, as seen in Figure 3.

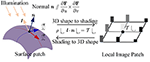
Figure 3. The consistency mapping equivalence between embedding F and the epitome intensity.

Nosotros refer to Equations (5) and (6) as 0th- and 1st- lodge consistence equations in 3D surface reconstruction respectively. More often than not, researchers solve any i of the 2 consistence problem to reconstruct 3D surface, classically, by multi-view stereo (Seitz et al., 2006) for 0th-order consistence problem, or by photometric stereo (Barsky and Petrou, 2003) for the 1st-gild one.

3.2. Embedding F

At that place are several types of representation for embedding F, such every bit detached mesh and C ⁱⁱ parametric surface. In fact the representation type of F also affects the reconstruction effect. Intuitively for mesh, on one hand there exists mapping deviation of rays from epitome points to vertices of mesh, which contributes to inaccurate texture charts ${\left\{{{T}}_i\right\}}_{i=1:\mathrm{north}}$ and affects the accuracy of reconstruction. On the other, detached differential operator, i.east., LBO (Meyer et al., 2003), brings potential distortion error when there exists obtuse triangles in the mesh caused by error local normal. Additionally, the precision of mesh likewise limit the particular of reconstruction.

Nosotros consider to apply C ² parametric surface as the representation of face up. More often than not, B-spline surface is recommended considering of its advantages of good locality over other types of surfaces such every bit polynomial surface and Bessel surface. By B-spline surface, it doesn't exist mapping deviation in geometric optics, and it avoids the potential distortion brought by discrete differential operator. Therefore, authentic and continuous back projection texture charts ${\left\{{{T}}_i\right\}}_{i=1:n}$ can be generated based on Equations (two), (3), and (5). Then accurate reconstruction can be implemented based on Equation (six). What's more, the precision tin can be enhanced for high-detailed reconstruction by inserting control points.

4. B-Spline Confront Embedding F, and the 0th-, 1st-, 2d–Gild Representation

The human face is assumed to be a uniform B-spline surface ${S}$ of degree 4 × four, with B = { b _mn } _M×N as its command points. In parameter domain ${U}$, knots $U={\left\{u_m\right\}}_{\mathrm{thou}=1}^{\mathrm{Thou}+\mathrm{four}}$ and $V={\left\{v_n\right\}}_{n=1}^{\mathrm{Northward}+\mathrm{four}}$ separate uv parameter plane into uniform grid. Allow u announce parameter point (u, five). The surface function is

$\text{F}(\text{u})={\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{n=1}^N}{R}_{g,n}(\text{u})b_{\mathrm{thousand}\mathrm{due\; north}},$

with R _m,n (u) = N _m,4(u) · N _{due north,4}(v) and

$\{\begin{array}{c}{\mathrm{North}}_{i,1}(\mathrm{west})=\{\begin{array}{ll}1& u_i\le w<u_{i+1},\\ 0& otherwi\mathrm{due\; south}\mathrm{due\; east},\end{array}\\ {\mathrm{Northward}}_{i,j}(\mathrm{westward})=\frac{(\mathrm{due\; west}-u_i)·N_{i,j-\mathrm{ane}}(\mathrm{westward})}{u_{i+j-1}-u_i}+\frac{(u_{i+j}-\mathrm{westward})·{\mathrm{Northward}}_{i+1,j-\mathrm{one}}(w)}{u_{i+j}-u_{i+1}},(j=4,3,2).\end{array}$

F is C ², meaning that it tin approximate the true shape in capricious uv precision with deterministic thou-ordered partial derivative $\frac{{\partial }^k\text{F}}{\partial u^{\mathrm{yard}}}$ and $\frac{{\partial }^{\mathrm{thousand}}\text{F}}{\partial {\mathrm{five}}^k}$, thousand = 1, 2, and $\frac{{\partial }^2\text{F}}{\partial u\partial v}$.

4.1. 0th-Social club Representation

Nosotros give a more than brief formulation of 0th-society representation as follows:

where b denotes a 3MN × i vector storing B-spline control points, and T| _u denotes a thin 3 × 3MN matrix stacking the 0th-lodge coefficients at parameter $\text{u}\in {U}$.

In fact, we needn't consider all 3D points mapping to 2D images when estimating a operator Π. Instead, we only consider f landmark points on human face up as shown in Figure 4, and their brief formulation is

$\begin{array}{ll}\text{F}{|}_{\text{u}(l_i)}=\text{T}{|}_{\text{u}({\mathrm{50}}_i)}·b,i=\mathrm{ane},\mathrm{two},\dots ,f,& (8)\end{array}$

where u(l _i ) is the parameter signal of the i-th feature point, i = 1, ii, …, f. The landmarks cover a sparse construction of confront.

Figure 4. Face construction divers by 40 feature points: the left side shows the point positions in a face image; the right side shows the structure topology with center center points of O _ane (−25, 0, 0) and O _ii (25, 0, 0) in iiiD space, which looks like a frontal second face structure from the direction of normal (0, 0, 1). (The face image used in the figure comes from LFW database¹).

four.two. 1st-Lodge Representation

The 1st-order partial derivatives of F w.r.t u and v are

$\begin{array}{l}{\text{F}}_u^{\prime }(\text{u})={\displaystyle \sum _{m=1}^{\mathrm{Chiliad}}}{\displaystyle \sum _{n=1}^N}{N}_{m,\mathrm{four}}^{\prime }(u)·N_{n,\mathrm{iv}}(v)b_{mn}\\ ={\displaystyle \sum _{\mathrm{chiliad}=1}^M}{\displaystyle \sum _{n=1}^N}(\frac{\mathrm{iv}}{u_{m+4}-u_i}{N}_{m,3}^{\prime }(u)-\frac{4}{u_{m+\mathrm{v}}-u_{k+1}}{N}_{\mathrm{1000}+\mathrm{ane},3}^{\prime }(u))·N_{n,4}(v)b_{mn}\end{array}$

and

$\begin{array}{l}{\text{F}}_v^{\prime }(\text{u})={\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{n=1}^N}{\mathrm{Northward}}_{m,4}(u)·N_{n,4}^{\prime }(v)b_{m\mathrm{northward}}\\ ={\displaystyle \sum _{m=1}^{\mathrm{1000}}}{\displaystyle \sum _{n=1}^N}{\mathrm{Northward}}_{m,\mathrm{four}}(u)·(\frac{4}{u_{n+4}-u_{\mathrm{north}}}{N}_{\mathrm{due\; north},3}^{\prime }(\mathrm{five})-\frac{4}{u_{n+5}-u_{n+\mathrm{i}}}{N}_{n+1,3}^{\prime }(v))b_{m\mathrm{north}}\end{array}$

respectively.

Similarly, we give a more than brief conception of 1st-gild fractional derivative as follows:

$\begin{array}{ll}\{\begin{array}{l}{\text{F}}_u^{\prime }{|}_{\text{u}}={\text{T}}_1{|}_{\text{u}}·\text{b}\\ {\text{F}}_{\mathrm{five}}^{\prime }{|}_{\text{u}}={\text{T}}_2{|}_{\text{u}}·\text{b}\end{array},& (\mathrm{ix})\end{array}$

where T ₁| _u and T ₂| _u denote the matrixes stacking the 1st-society coefficients due west.r.t u and v, respectively.

Therefore, the surface normal vector at u tin can be computed by the cantankerous product

$\begin{array}{ll}\mathrm{northward}{|}_{\text{u}}=\frac{{\text{F}}_u^{\prime }{|}_{\text{u}}\times {\text{F}}_v^{\prime }{|}_{\text{u}}}{\left|\right|{\text{F}}_u^{\prime }{|}_{\text{u}}\times {\text{F}}_v^{\prime }{|}_{\text{u}}\left|\right|}=s{|}_{\text{u}}·{\text{F}}_u^{\prime }{|}_{\text{u}}\times {\text{F}}_{\mathrm{five}}^{\prime }{|}_{\text{u}},& (10)\end{array}$

which is the central data for detailed reconstruction using photometric stereo method.

four.three. 2nd-Order Representation

And similarly, the 2d-guild partial derivatives w.r.t. u and v, respectively are

$\begin{array}{ll}\{\begin{array}{l}{\text{F}}_{uu}^{″}{|}_{\text{u}}={\text{T}}_{11}{|}_{\text{u}}·\text{b}\\ {\text{F}}_{vv}^{″}{|}_{\text{u}}={\text{T}}_{22}{|}_{\text{u}}·\text{b}\end{array},& (11)\end{array}$

where T _eleven| _u and T ₂₂| _u denote the matrixes stacking the 2nd-order coefficients w.r.t u and v, respectively. The second-order information tin be used for smooth control during optimization.

Based on face surface embedded with B-spline function, we present the pinpoint 0th- and 1st-society geometric consistency conditions in the following department.

v. Consistency Modeling in B-Spline Confront Reconstruction

Reconstruction problem is to compute F past solving 0th-order consistence of Equation (five) or 1st-guild consistence of Equation (6). Generally, two consistency conditions are combined for face reconstruction because that estimating abundant consequent points in images is express and that the estimated normals are unfaithful. Furthermore, how to obtain the authentic registration of 0th- and 1st-order data is the near important to high-detailed B-spline reconstruction.

The well-registered textures are depression-rank structures of the back projection texture charts. Just in do, they can be hands violated due to the presence of partial occlusions or expressions in the images captured. Since these errors typically impact just a small fraction of all pixels in an chart, they can exist modeled as sparse errors whose nonzero entries can have arbitrarily big magnitude.

five.1. Modeling Occlusion and Expression Corruptions in 0th-Order Consistence

Let e _i correspond the error corresponding to epitome I _i such that the back projection texture charts ${{T}}_i={(I_i◦{\tau }_i^{-\mathrm{i}})}^{\#}-{\mathrm{east}}_i={{T}}_i^e-{\mathrm{due\; east}}_i,i=\mathrm{one},\mathrm{two},\dots ,n$ are well registered to the surface F, and free of any corruptions or expressions. As well combining with 0th-order representation of B-spline face in Equation (7), the formulation (five) can be modified every bit follows:

$\begin{array}{ll}\begin{array}{l}<\widehat{\text{b}},\left\{{\widehat{\Pi }}_i\right\},\widehat{\text{D}},\widehat{\text{E}}>=arg\underset{\text{b},\left\{{\Pi }_i\right\},\text{D},\text{E}}{\text{lim}}||\text{D}|{|}_{*}+\eta ||\text{E}|{|}_{\mathrm{i}},\\ \mathrm{southward}.t.\left|\right|{\text{D}}^{\mathrm{eastward}}-\text{D}-\text{Due east}|{|}_F\le \epsilon .\end{array}& (12)\end{array}$

where ${\text{D}}^{\mathrm{due\; east}}=\left[\text{vec}({{T}}_{\mathrm{i}}^{\mathrm{eastward}}),\text{vec}({{T}}_{\mathrm{two}}^{\mathrm{due\; east}}),\dots ,\text{vec}({{T}}_{\mathrm{due\; north}}^e)\right]$ and Eastward = [vec(e ₁), vec(e _ii), …, vec(e _n )].

Withal, the solution $\widehat{\text{b}}$ of face surface ${S}$ is not unique if all images are in similar views. And the reconstruction is not high-detailed even if we can brand a unique solution by applying a prior face up template. And then we also need to model high details in 1st-gild consistence.

5.ii. Modeling Loftier Details in 1st-Guild Consistence

The resolution of reconstruction is determined past the density of correctly estimated normals. To enhance the resolution of B-spline surface, we apply operator (·)^# to sample Due north _p dense parameter points {u _j } _{j=1 : N p} on the domain ${U}$ for the problem of Equation (half-dozen).

So the well-registered and dumbo texture are obtained past

for i = 1, 2, …, n and j = i, 2, …, North _p .

Co-ordinate to Lambertian illumination model seen in Equation (half dozen), dense normals n _j as well as low-cal l _i tin can be computed from the shading (intensity) of charts ${{T}}_i$ by SVD method.

Finally, the high detailed reconstruction must satisfy

$\begin{array}{ll}\underset{\text{F}}{\text{min}}{\displaystyle \sum _{j=\mathrm{ane}}^{N_p}}||{\text{north}}_j-\mathrm{southward}{|}_{{\text{u}}_j}{\text{F}}_u^{\prime }{|}_{{\text{u}}_j}\times {\text{F}}_v^{\prime }{|}_{{\text{u}}_j}|{|}_2^{\mathrm{two}}.& (14)\end{array}$

By putting Equation (9) into Equation (xiv), we go

$\begin{array}{ll}\underset{\text{b}}{\text{min}}{\displaystyle \sum _{j=1}^{N_p}}||{\text{north}}_j-\mathrm{south}{|}_{{\text{u}}_j}({\text{T}}_1{|}_{{\text{u}}_j}·\text{b})\times ({\text{T}}_2{|}_{{\text{u}}_j}·\text{b})|{|}_{\mathrm{ii}}^2.& (15)\end{array}$

Weather condition of both Equations (6) and (15) have to be considered for a adept reconstruction, which is very difficult. Therefore, nosotros propose a practical solution that combining both 0th- and 1st-order consistence.

6. Applied Solution Combining 0th- and 1st-Order Consistence

The bug of both 0th-society consistence and 1st-club consistence are difficult to solve. For , Jacobian matrices w.r.t. ${\left\{{\tau }_i^{-1}\right\}}_{i=1:\mathrm{due\; north}}$ accept to exist computed, which is computing-expensive. And the solution of Equation (xv) is not unique, either. Therefore, nosotros aim to detect a applied solution to handle both two consistence weather condition in this section. We get-go define the subproblem for each condition, and then provide a iterative algorithm.

6.i. 0th-Order Solution

In Equation (6), three kind of parameters including camera parameters {Π _i } _{i=ane : n} , surface parameters F (or b), and texture parameters ${\left\{{{T}}_i\right\}}_{i=1:n}$ (or D) need to be computed, but they are difficult to be solved simultaneously. Nosotros adopt to optimize them by turns, instead.

6.1.1. Estimating Π _i

According to linear transformation from 3D to 2D in Equation (1), nosotros can gauge calibration s _i , rotation R _i and translationt _i of landmarks for each image I _i , i = one, 2, …, northward based on the and SVD method (Kemelmacher and Seitz, 2011). The image landmarks are detected past a state-of-art detector (Burgos-Artizzu et al., 2013) that has a like high functioning to man. And the 3D landmarks are defined on a B-spline face template with control point parameter b ₀, co-ordinate to Equation (8).

6.ane.two. Estimating b

Let f denote a twonf × 1 vector stacking f landmarks of north images, and P denote a 2nf × 3f projection matrix stacking north views of parameters s _i R _{i, [1,ii]}, and t denote a twonf × 1 vector stacking f translation. The update of b tin can exist implemented by solving:

$\begin{array}{ll}\underset{b}{\text{min}}\left|\right|\text{f}-\text{t}-\text{P}·{\text{T}}^{\#\mathrm{50}}\text{b}|{|}_{\mathrm{two}}^2+\zeta |\left|({\text{T}}_{11}^{\#}+{\text{T}}_{22}^{\#})(\text{b}-{\text{b}}_0)\right|{|}_{\mathrm{two}}^2& (16)\end{array}$

where the first and the second are 0th- and 2nd-club item, respectively, and ζ is used to remainder them. Operator (·) ^#l is a sampling operator that selects B-spline coefficients of landmarks at parameters {u(l _i )} _{i=1 : f} , and (·)^# selects B-spline coefficients at {u _j } _{i=i : N p} . In fact, T ^#l is a threef × threeMN matrix that stacks T| _{u(fifty i )}, i = 1, 2, …, f, and ${\text{T}}_{11}^{\#}$ (or ${\text{T}}_{22}^{\#}$) is a threef × 3MN matrix that stacks T _eleven| _{u j} (or T ₂₂| _{u j} ), j = 1, 2, …, Due north _p .

The second item also piece of work as a regularization measuring the altitude of local information between faces b and b ₀. It helps eliminate touch on of geometric rotation brought by 0st-society warping, and guarantee a smoothness changing during optimization. Specially, ζ cannot exist too small, otherwise a fast changing may bring a local optimal.

half-dozen.1.three. Estimating ${{T}}_i$

${\tau }_i^{-1}$ and τ _i is determined by Equation (2) when Π _i and b is known. And so texture chart with racket is obtained by applying consequent parameter sampling ${{T}}_i^e={(I_i◦{\tau }_i^{-1})}^{\#}$. Let ${\text{D}}^e=\left[\text{vec}({{T}}_{\mathrm{i}}^e),\text{vec}({{T}}_{\mathrm{two}}^e),\dots ,\text{vec}({{T}}_{\mathrm{due\; north}}^e)\right]$. The update of texture charts is to minimize the following formulation

$\begin{array}{ll}\begin{array}{l}<\widehat{\text{D}},\widehat{\text{E}}>=arg\underset{\text{D},\text{E}}{\text{lim}}||\text{D}|{|}_{*}+\eta ||\text{Eastward}|{|}_1,\\ s.t.||{\text{D}}^{\mathrm{east}}-\text{D}-\text{Eastward}|{|}_F\le \epsilon .\end{array}& (17)\end{array}$

which tin can exist solved by Robust PCA (Bhardwaj and Raman, 2016). And let ${{T}}_i{|}_{{\text{u}}_j}={\widehat{\text{D}}}_{ji}$, for i = 1, 2, …, north, and j = 1, 2, …, N _p .

half-dozen.2. 1st-Lodge Solution

Firstly, texture charts based photometric stereo method is used to approximate the local normals. Secondly, a normals driven optimization strategy is proposed to optimize the B-spline face.

half dozen.2.1. Estimating north _j

Co-ordinate to Photometric stereo, the shape of each point tin exist solved by the observed variation in shading of the images. Data of n texture charts are input into Yard _{due north×N p} for estimating the initial shape $\widetilde{\mathrm{Due\; south}}$ and lighting $\tilde{L}$ past factorizing Thou = LS via SVD (Yuille et al., 1999). $\widetilde{\mathrm{50}}=U\sqrt{\Sigma }$ and $\widetilde{\mathrm{Southward}}=\sqrt{\Sigma }{V}^T$, where Chiliad = UΣV ^T . To approach the truthful normal information, we estimate the shape Southward and ambiguity A past post-obit the piece of work of Kemelmacher and Seitz (2011). Lastly, the normal at j-th point is ${\mathrm{northward}}_j={\mathrm{Due\; south}}_j^T$, where Southward _j is the j-thursday row of S.

6.ii.2. Estimating b

Nosotros normalize n _j and stack them into a 3North _p × i vector h. Equation (fifteen) tin be rewritten as

${\text{O}}_1=\underset{\text{b}}{\text{min}}\left|\right|\text{h}-\Lambda {|}_{\text{b}}·(({\text{T}}_1^{\#}\text{b})\otimes (({\text{T}}_2^{\#}\text{b}))|{|}_2^{\mathrm{ii}},$

where Λ is a 3N _p × 3Northward _p diagonal matrix that stores 3Northward _p reciprocals of lengths of the normals { n _j } _{j=1 : N p} ; and (·)^# is a selection operator that selects threeN _p rows of 1st-order coefficients at parameter {u _j } _{j=1 : North p} ; and b ₀ represent the control points of a B-spline template face. Specially, symbol ⊗ denotes a composite operator of cantankerous production, which makes w ⊗ v = [ w _i × v ₁; west ₂ × v _two; …; west _{Northward p} × v _{N p} ], where w and 5 are threeNorth _p × 1 vectors containing N _p normals.

However, there exists 2 issues: (1) the low-dimension h may non guarantee an unique solution of loftier-dimension b ; and (ii) the system is non simply linear, which is difficult to exist solved. Therefore, a frontal constraint based on template b ₀ is practical to make a unique solution; And a strategy of approximating to linearization is also proposed to brand a linear solution.

6.2.2.1. Frontal Constraint

The frontal constraint is a distance measurement condition between surface ${S}$ and template w.r.t. ten- and y-component:

where the matrix T ^#xy stacks 0th-order coefficients at parameter {u _j } _{j=1 : North p} corresponding to x- and y- components. Operator (·) ^#sxy also sets the coefficients corresponding to z- components to zeros.

Particularly, the commencement detail O ₁ is non a simple linear form, for which an approximating to linearization is proposed.

6.2.2.ii. Approximating to Linearization

According to the characteristics of the cantankerous-production ⊗, the outset item in O ₁ can be rewritten every bit a linear-similar formulation:

$||\text{h}-L{|}_{\text{b}}·\text{b}|{|}_{\mathrm{two}}^2\text{ or}||\text{h}-R{|}_{\text{b}}·\text{b}|{|}_2^2,$

where $\{\begin{array}{l}L{|}_{\text{b}}=\Lambda {|}_{\text{b}}·{\left[{\text{T}}_1^{\#}\text{b}\right]}_{\otimes }·{\text{T}}_2^{\#}\\ R{|}_{\text{b}}=-\Lambda {|}_{\text{b}}·{\left[{\text{T}}_2^{\#}\text{b}\right]}_{\otimes }·{\text{T}}_{\mathrm{i}}^{(sn)}.\end{array}$

Particularly, the operation [·]_⊗ makes a 3Due north _p × 1 vector $\mathrm{west}={\left[w_{\mathrm{i}}^T,w_2^T,\dots ,w_{{\mathrm{Northward}}_p}^T\right]}^T$ become a 3N _p × 3N _p sparse matrix [ west ]_⊗ = diag([ w ₁]_×, [ w ₂]_×, …, [ w _{Due north p} ]_×), where ${\left[w_i\right]}_{\times }=\left[0,-w_i^z,w_i^y;w_i^z,0,-w_i^x;-{\mathrm{west}}_i^y,{\mathrm{due\; west}}_i^{\mathrm{ten}},0\right],i=1,\mathrm{ii},\dots ,{\mathrm{Due\; north}}_p.$

If b is a known parameter, due east.k., equally b ₀, for 50 | _b , the minimization of ||h − L | _{b 0} · b|| volition exist a linear system. That is as well true for R | _b .

In fact, nosotros can use formulation ||h − L | _{b 0} · b|| to optimize the control points in parameter space of 5 by fixing u, and utilize ||h − R | _{b 0} · b|| to optimize in parameter space of u by fixing five.

Algorithm 1. Iterative Algorithm for B-spline Confront Optimization

A practical skill is to optimize the control points on u and v parameter spaces past turns. The ii iteration items are rewritten equally

$\{\begin{array}{l}\left|\right|\text{h}-L{|}_{{\text{b}}_0}·\text{b}|{|}_2^{\mathrm{ii}}+\lambda ||{\Lambda }_{\mathrm{one}}{|}_{{\text{b}}_0}·{\text{T}}_1^{\#}·(\text{b}-{\text{b}}_0)|{|}_2^{\mathrm{two}},\\ \left|\right|\text{h}-R{|}_{{\text{b}}_0}·\text{b}|{|}_2^2+\lambda ||{\Lambda }_2{|}_{{\text{b}}_0}·{\text{T}}_{\mathrm{two}}^{\#}·(\text{b}-{\text{b}}_0)|{|}_2^{\mathrm{two}}.\end{array}$

where the 2nd term for each formulation is unit tangent vector constraint on the fixed the directions. Λ_ane| _{b 0} (or Λ₂| _{b 0} ) is a iiiN _p × 3N _p diagonal matrix that stores 3Due north _p reciprocals of lengths of tangent vector $\frac{\partial \text{F}}{\partial u}$ (or $\frac{\partial \text{F}}{\partial v}$) at {u _j } _{j=1 : N p} . During this procedure b ₀ is updated step-by-step. As shown in Figure five, two fractional derivatives $\frac{\partial \text{F}}{\partial v}$ and $\frac{\partial \text{F}}{\partial u}$ at (u, v) are updated until $\frac{\partial \text{F}}{\partial v}\times \frac{\partial \text{F}}{\partial u}$ converges to n .

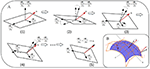
Figure v. Iterative adjustment on two fractional derivatives: Procedure (ane) to (2) adjusts $\frac{\partial F}{\partial u}$ by fixing $\frac{\partial F}{\partial v}$, and process (3) to (4) adjusts $\frac{\partial F}{\partial \mathrm{five}}$ by fixing $\frac{\partial F}{\partial u}$, … until that $\frac{\partial F}{\partial u}\times \frac{\partial F}{\partial v}$ is infinitely close to objective north ; Process A implements a practically and iteratively linear handle for B-spline surface adjustment in B.

By integrating with O _ii, the last formulation of optimization consists of two items equally follows:

$\begin{array}{ll}\{\begin{array}{c}\underset{\text{b}}{\text{min}}\left|\right|\left[\begin{array}{c}\text{h}\\ {\text{T}}^{\#\mathrm{ten}y}{\text{b}}_0\end{array}\right]-\left[\begin{array}{l}L{|}_{{\text{b}}_0}\\ {\text{T}}^{\#xy}\end{array}\right]\text{b}|{|}_{\mathrm{two}}^{\mathrm{two}}+\lambda \left|\right|{\Lambda }_1{|}_{{\text{b}}_0}·{\text{T}}_1^{\#}(\text{b}-{\text{b}}_0)|{|}_2^2,(a)\\ \underset{\text{b}}{\text{min}}\left|\right|\left[\begin{array}{c}\text{h}\\ {\text{T}}^{\#xy}{\text{b}}_0\end{array}\right]-\left[\begin{array}{l}R{|}_{b_0}\\ {\text{T}}^{\#xy}\end{array}\right]\text{b}|{|}_{\mathrm{ii}}^{\mathrm{ii}}+\lambda \left|\right|{\Lambda }_2{|}_{{\text{b}}_0}·{\text{T}}_2^{\#}(\text{b}-{\text{b}}_0)|{|}_{\mathrm{ii}}^2.(b)\end{array}& (\mathrm{eighteen})\end{array}$

The b ₀ is initialized past value of b ₀. Then nosotros tin solve b and update b ₀ orderly by minimizing (a) and (b) in Equation (18) iteratively until convergence.

6.3. Algorithm

An iterative algorithm is presented for this practical solution in Algorithm i. Processes of 0th-order consistence and 1st-society consistence are separately conducted in the inner loop. And the outer loop guarantees a global convergence on 2 consistence problem.

half dozen.three.i. Computational Complication

The computation in above Algorithm 1 involves linear least square for solving Equations (16), (eighteen.a), and (eighteen.b), SVD for estimating photographic camera parameter, and Robust PCA for Equation (17). In detail, the computational complication for solving Equation (sixteen) is O(n ^two f ² MN), and that of both Equations (18.a) and (18.b) are O(${\mathrm{Due\; north}}_p^{\mathrm{ii}}KN$). The computational complication of robust PCA comes to be O($N_p^{\mathrm{two}}k$), where k is the rank constraint. By assuming Due north _p > M > N >> f > n, computational complexity of the other parts can be negligible. In addition, nosotros need considering the number of iteration for total computation of Algorithm 1.

7. Experiment

In this department experiments are presented to verify our automatic free-form surface modeling method. We start describe the pipeline to prepare a drove of confront images of a person for B-spline face reconstruction. And so nosotros demonstrate the quantitative and qualitative comparisons with recent baseline methods on projected standard images from ground truth 3D data (Zhang et al., 2017) with various expressions, illuminations and poses. Finally, we conduct challenging reconstructions and comparison based on real unconstrained data taken from the challenging Labeled Faces in Wild (LFW) database^one (Huang et al., 2007).

7.1. Data Pipeline and Evaluation

seven.1.i. Synthesized Data With Expression

The ground truth data are from the space-times faces (Zhang et al., 2017) which contains 3D face models with different expressions. We use the data because information technology is convenient to evaluate our method with ground truth. And different poses and illuminations can also exist simulated by the spaces-times faces, seen in Figure 6. Images with diverse poses and illuminations are collected, and characteristic points manually labeled. The reconstruction is evaluated by the error to the footing truth model.

Figure 6. Sample information fake by the spaces-times faces (Zhang et al., 2017) : images and 3D model with various poses and illuminations are available; information of sample S1, S2, S3, and S4 are used for evaluation.

vii.1.ii. Real Data in the Wild

The wild information (Huang et al., 2007) has characteristics of subject field variations, illumination changes, various pose, background ataxia and occlusions. Images of each person are nerveless and input into a facial point detector (Burgos-Artizzu et al., 2013) that has a similar high performance to human, to find the forty facial points shown in Figure 4. The initial B-spline template face is computed from a neutral model of space-time faces.

vii.1.three. Comparison

To verify the accuracy of automatic surface reconstruction, discrete points are sampled from the generated continuous gratuitous-form shape, and are compared to the traditional discrete reconstructions, e.k., work by Kemelmacher and Seitz (2011) and Roth et al. (2015). For a memory-limited capture organisation, information technology is not available to collect thousands of images as what Kemelmacher and Seitz (2011) and Roth et al. (2015) have done, so we limit all the reconstructions to less than 40 images. We as well compare them with an terminate-to-end deep learning method by Sela et al. (2017) qualitatively. Deep learning methods rely preparation on a large corporeality of unconstrained data, and then we simply use the model provided by Sela et al. (2017) that accept been preparation on unconstrained images, and examination information technology on the images in the wild.

seven.2. Synthesized Standard Images

We conduct five sessions of reconstructions: the start 4 are used to reconstruct expression S1, S2, S3, and S4 by using their corresponding images, and the fifth session S5 is based on images with different expressions. Each session contains forty images with various illumination and different poses. Reconstruction results are compared with the re-implemented method Kemel_meth by Kemelmacher and Seitz (2011) and Roth_meth by Roth et al. (2015). Kemel_meth generates frontal face surface based on integration in image domain of size 120 × 110. We prune it co-ordinate to the peripheral facial points and interpolate points to get more than vertices. Roth_meth generates a face mesh based on a template with 23,725 vertices. In our method, command point filigree of 102 × 77 is optimized for a B-spline confront surface.

seven.2.1. Quantitative Comparison

To compare the approaches numerically, we compute the shortest point-to-point distance from footing truth to reconstruction. Point clouds are sampled from B-spline confront and aligned according to absolute orientation problem. Every bit done in work of Roth et al. (2015), mean Euclidean distance (MED), and the root mean foursquare (RMS) of the distances, after normalized by the center-to-eye altitude, are reported in Table one. Particularly, evaluation of Roth_meth is based on surface clipped with same facial points similar the other 2 methods by considering a off-white comparing. In the tabular array, the all-time results are highlighted in boldface, and the underlined issue has no meaning deviation with the best. To our knowledge, Roth_meth is the state-of-art method for face reconstruction from unconstrained images. Its re-implementation version is afflicted by the noisy normal estimation because of limited number images, showing results that are not good like as in its original paper. But it still performs proficient on all sessions. As a whole, results by both Roth_meth and our method have lower errors than Kemel_meth. On session S1 and S5, Roth_meth obtains the lowest hateful mistake 5.21 and 6.96%, respectively. Withal, we obtains lower RMS 4.10 and 4.34% while its errors is quite close to the all-time particularly on session S5. And on session S2, S3, and S4, our method obtains the best results, 6.49 ± 4.66, 4.43 ± two.91, and 6.46 ± iv.06%. In contrast, the errors by Kemel_meth exceed 8%, and the RMS is as well very large on every session. These numerical comparisons supply highly persuasive bear witness that our B-spline method tin can build promising reconstructions based on face images.

Table 1. Distances of the reconstruction to the ground truth.

7.two.2. Visual Comparison

The visual results in Figure 7. We prove 3D models in mesh format for three methods on different sessions, and vertex numbers of models are also presented. It also demonstrates that our method has a promise performance past comparisons in the figure. An important fact is that Kemel (Kemelmacher and Seitz, 2011) cannot brand a credible depth information and global shape, e.g., the global shape of reconstruction S2 and the mouse and nose of S3 are plain incorrect, only our method solves global and local trouble by optimization of 0th- and 1st-order consistency. And while Roth (Roth et al., 2015) generates more detailed information of an individual, it also produces baloney at the detailed shape, e.chiliad., the center of reconstruction S2 and the nose of reconstruction S3 and S4. In contrast, our method obtains realistic shape both globally and locally.

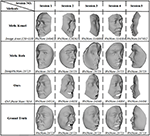
Figure 7. Visual reconstructions and comparisons for session S1, S2, S3, S4, and S5: for each session of reconstructions, a column lists the 3D results of Kemelmacher and Seitz (2011), Roth et al. (2015), and the states, too equally basis truth. (VrxNum means vertex number; TempVtxNum means vertex number of template; and Ctrl.Point Num means the control point number of B-spline confront surface. Particularly, the vertices of B-spline face are points sampled from the reconstructed parametric surface).

7.2.3. Characteristic Comparison

We requite statistics of characteristics of the results generated by the three methods in Table 2, covering the global shape, local detail, apparent depth, smoothness, distortion, and derivability. Depending on the quantitative and qualitative comparisons, nosotros also give a rough rating. 1 star, two stars, and iii stars represents bad, general, and skilful reconstruction respectively in the rating arrangement. Both Roth_meth and our method obtain skillful scores on global shape, local item, and credible depth. And both Kemel_meth and our method obtain a good score on smoothness. Because of the bad depth, Kemel_meth also gets bad score on global shape and distortion, and gets general scores on local detail. In add-on, B-spline face up model has better smoothness than the models by Kemel_meth and Roth_meth, because it is C ^two differentiable parametric surface while the other 2 are discrete model. Conclusively, 0th- and 1st-lodge consistency modeling using B-spline surface is efficient to reconstruct parametric surface of individual face up.

Table two. A characteristics summarization of three methods by crude rating with number of ✰.

7.3. Existent Unconstrained Images

Our method is also tested based on existent unconstrained information. Unconstrained data hateful that the images are captured nether uncertain status, and the faces in the images are dissimilar in expression, pose and illumination status. It is hard to build the geometrical consistency for reconstruction using such data. Unlike the experiments in the work by Kemelmacher and Seitz (2011) using hundreds of images, we acquit reconstruction with limited number of images, because a large mountain of face images for one person are not always available for small sample size tasks such as criminal investigation. In the experiment, uniformly 35 images are collected for each person from LFW database¹ covering different poses, illuminations and expressions.

Visual face reconstructions for Colin Powell, Donald Rumsfeld, George W. Bush, Hugo Chavez, and Gloria Macapagal Arroyo are compared with other two methods, equally shown in Effigy eight. Permit A label the results generated by the reimplemented Kemel_meth, and let B label the results generated by the reimplemented Roth_meth, and permit C label the method Seta_meth of deep learning by Sela et al. (2017) and let D label our results. Particularly, the input for Seta_meth is one image selected from the 35 images. Images in column 1, v, and 8 are corresponding mean textures and 2 views of images respectively. By comparing these results, we find some phenomena equally follows:

(one) In frontal viewpoint, A and D show more vivid details than B, e.g., eyes and nose of Colin Powell. But in an other viewpoint, D shows more credible shape than A, e.g., the optics and the brow of Colin Powell, and the forehead and the mouth of Donald Rumsfeld.

(ii) When the normals are incorrectly estimated from a limited number of images, e.g., for Gloria Macapagal Arroyo, A loses the local information completely, just B, C, and D yet maintain general geometrical shape of face. For all methods, reconstructing nose is a challenge considering the geometric curvature of the nose varies greatly. When the images are not enough, the racket could be amplified. So B shows bad results at olfactory organ existence express by number of input images.

(3) The input of C is a approximately frontal face up paradigm selected. As the model of C is learning on a set of 3D confront data, information technology may not handle the uncertain noise and identity of inputs. So the details in reconstruction by C don't look existent, although their global shapes are stable and like human faces.

(4) By comparison, our method steadily produces better looking results than others from different viewpoints in the dataset. Clear and vivid details can be seen at key components such as eyes, nose and mouth, forehead, and cheek.

Figure 8. Visual reconstructions and comparisons for Colin Powell, Donald Rumsfeld, George W. Bush, Hugo Chavez, and Gloria Macapagal Approach: (1) Images in cavalcade 1, v, and 9 are respective mean textures and ii views of images, respectively; (two) Columns labeled by A show the results generated by the reimplemented Kemel_meth, and columns labeled by B testify the results generated past the reimplemented method Roth_meth, and columns labeled by C evidence the results generated by the Seta_meth, and columns labeled past C show our results. (The face images used in the effigy come up from LFW database¹).

8. Give-and-take

All the to a higher place experiments prove that our method tin build pinpoint geometrical consistency on the express number of existent unconstrained data. Our method may non be all-time method in area of 3D reconstruction from multiple images, as the results in the original work by B looks better. Information technology could deal with 3D reconstruction with express number of images. Considering we may not obtain big amount of images for reconstruction as washed by Roth et al. (2015), for some condition restricted system. The shortcomings of A are mainly resulted from the inauthentic depth generated past integration method. And the bad results of B are caused past that the mesh template cannot build correct geometric consistency of number limited of unconstrained images and that the discrete differential operating on estimated noisy normal brings distortion errors. In contrast, we build pinpoint geometric consistency using B-spline surface. B-spline can smooth the noise in estimated normal amend. And then D can reconstruct right confront shape with little distortion, showing better event as a whole.

In the comparison, we don't consider other deep learning methods based methods appeared in recent years (Dou et al., 2017; Richardson et al., 2017; Lin et al., 2020; Sengupta et al., 2020; Shang et al., 2020). Considering almost all recent works are focused on deep learning methods for single prototype based 3D face reconstruction (Dou et al., 2017; Richardson et al., 2017; Lin et al., 2020; Sengupta et al., 2020), as well as using a 3DMM model as prior. And the multi-view deep learning method only handle constrained face up images (Shang et al., 2020). It means the deep learning methods can employ a large amount of training information, and also a good prior. The input are different betwixt these learning based methods and our method. Then we bear comparison with the archetype optimization-based approaches for the sake of fairness. Even so, we too select one representative method by Sela et al. (2017) to show result past deep learning as a reference in the comparison. It proves that if the test are not satisfactory to the prior and distribution of training data, it may obtain bad result.

9. Conclusions

This study fix out to present high-detailed face up reconstruction from multiple images based on pinpoint 0th- and 1st-gild geometric consistence using B-spline embedding. Based on the good consistence modeling in geometric optics, the method works well for data with different poses and expressions in the wild. The key contribution of this study is that surface modeling adapts the correct rays in geometric optics by using B-spline embedding. This makes the high-detailed B-spline modeling from a number limited of confront images captured under wild status become reality. The method could also exist applied to expression tracking and assisting confront recognition in a monitoring or robot system.

Information Availability Statement

The original contributions presented in the study are included in the article/supplementary material, farther inquiries tin be directed to the respective author/due south.

Writer Contributions

WP and ZF has contributed equally to the core idea every bit well as the experiment design and results analysis. YS, KT, and CX has provided assistance in experiments and analysis, nether ZF's supervision. Besides, KT and MF provided the research group with fiscal support and experimental equipments. KT and ZF are supportive corresponding authors. All authors contributed to the article and canonical the submitted version.

Funding

This research was partly supported past Science and Engineering science Plan of Guangzhou, China (No. 202002030263), Shenzhen Science and Technology Foundation (JCYJ20170816093943197), Guangdong Basic and Applied Bones Research Foundation (2020A1515110997), National Natural Science Foundation of Cathay (Nos. 61772164 and 62072126), and National Key R&D Program of China (No. 2019YFB1706003).

Conflict of Interest

The authors declare that the inquiry was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnote

References

Agarwal, Southward., Furukawa, Y., Snavely, N., Simon, I., Curless, B., Seitz, S. Yard., et al. (2011). Building Rome in a day. Commun. ACM 54, 105–112. doi: 10.1145/2001269.2001293

CrossRef Full Text | Google Scholar

Artificial, L. A., and Aryananda, Fifty. (2002). "Recognizing and remembering individuals: Online and unsupervised face recognition for humanoid robot," in Proc. of IROS (Lausanne), 1202–1207.

Google Scholar

Barsky, S., and Petrou, Thousand. (2003). The 4-source photometric stereo technique for three-dimensional surfaces in the presence of highlights and shadows. IEEE Trans. Design Anal. Mach. Intell. 25, 1239–1252. doi: x.1109/TPAMI.2003.1233898

CrossRef Full Text | Google Scholar

Bhardwaj, A., and Raman, S. (2016). Robust PCA-based solution to image composition using augmented lagrange multiplier (ALM). Visual Comput. 32, 591–600. doi: 10.1007/s00371-015-1075-1

CrossRef Full Text | Google Scholar

Blanz, Five., Mehl, A., Vetter, T., and Seidel, H. P. (2004). "A statistical method for robust 3D surface reconstruction from thin data," in International Symposium on 3D Data Processing, Visualization and Transmission (3DPVT) (Thessaloniki), 293–300. doi: 10.1109/TDPVT.2004.1335212

CrossRef Full Text | Google Scholar

Blanz, 5., and Vetter, T. (1999). "A morphable model for the synthesis of 3D faces," in Proceedings of Conference on Calculator Graphics and Interactive Techniques (New York, NY), 187–194. doi: x.1145/311535.311556

CrossRef Total Text | Google Scholar

Burgos-Artizzu, Ten. P., Perona, P., and Dollár, P. (2013). "Robust face up landmark estimation under occlusion," in IEEE International Conference on Computer Vision (ICCV), (Sydney, VIC), 1513–1520. doi: ten.1109/ICCV.2013.191

CrossRef Full Text | Google Scholar

Carr, J. C., Beatson, R. One thousand., Cherrie, J. B., Mitchell, T. J., Fear, W. R., Mccallum, B. C., et al. (2001). Reconstruction and representation of 3D objects with radial ground functions. ACM Siggraph 67–76. doi: 10.1145/383259.383266

CrossRef Full Text | Google Scholar

Deng, Y., Yang, J., Xu, S., Chen, D., Jia, Y., and Tong, X. (2019). "Accurate 3D face reconstruction with weakly-supervised learning: From single image to image set," in IEEE Reckoner Vision and Pattern Recognition Workshops. Long Beach, CA. doi: 10.1109/CVPRW.2019.00038

CrossRef Full Text | Google Scholar

Dou, P., Shah, Southward. One thousand., and Kakadiaris, I. A. (2017). "End-to-end 3D face reconstruction with deep neural networks," in 2017 IEEE Conference on Computer Vision and Design Recognition (CVPR) (Honolulu, HI), 1503–1512. doi: 10.1109/CVPR.2017.164

CrossRef Total Text | Google Scholar

Gecer, B., Ploumpis, Due south., Kotsia, I., and Zafeiriou, South. (2019). "Ganfit: generative adversarial network fitting for loftier fidelity 3D confront reconstruction," in IEEE Computer Vision and Blueprint Recognition (CVPR) (Long Embankment, CA), 1155–C1164. doi: 10.1109/CVPR.2019.00125

CrossRef Full Text | Google Scholar

Gonzalez-Mora, J., De la Torre, F., Guil, North., and Zapata, East. L. (2010). Learning a generic 3D face model from 2D image databases using incremental construction-from-move. Image Vis. Comput. 28, 1117–1129. doi: 10.1016/j.imavis.2010.01.005

CrossRef Full Text | Google Scholar

Heo, J., and Savvides, M. (2009). "In between 3D active appearance models and 3D morphable models," in Computer Vision and Blueprint Recognition (Miami Beach, FL). doi: ten.1109/CVPRW.2009.5204300

CrossRef Full Text | Google Scholar

Hoch, M., Fleischmann, G., and Girod, B. (1998). Modeling and animation of facial expressions based on b-splines. Vis. Comput. 11, 87–95. doi: ten.1007/BF01889979

CrossRef Full Text | Google Scholar

Huang, Thou. B., Ramesh, M., Berg, T., and Learned-Miller, E. (2007). Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments. Technical Report 07-49, Academy of Massachusetts, Amherst.

Google Scholar

Kazhdan, M., Bolitho, G., and Hoppe, H. (2006). "Poisson surface reconstruction," in Proceedings Symposium on Geometry Processing (SGP) 06 (Goslar), 32.

Google Scholar

Kemelmacher Shlizerman, I. and Basri, R. (2011). 3d face reconstruction from a single image using a single reference face shape. IEEE Trans. Pattern Anal. Mach. Intell. 33, 394–405. doi: ten.1109/TPAMI.2010.63

PubMed Abstract | CrossRef Full Text

Kemelmacher Shlizerman, I. and Seitz, S. One thousand. (2011). "Face up reconstruction in the wild," in IEEE International Conference on Computer Vision (ICCV) (Barcelona), 1746–1753. doi: 10.1109/ICCV.2011.6126439

CrossRef Full Text | Google Scholar

Khraisat, A., Gondal, I., Vamplew, P., Kamruzzaman, J., and Alazab, A. (2019). A novel ensemble of hybrid intrusion detection arrangement for detecting internet of things attacks. Electronics 8:1210. doi: ten.3390/electronics8111210

CrossRef Full Text | Google Scholar

Koo, H.-South., and Lam, Yard.-Grand. (2008). Recovering the 3D shape and poses of face images based on the similarity transform. Pattern Recogn. Lett. 29, 712–723. doi: 10.1016/j.patrec.2007.11.018

CrossRef Full Text | Google Scholar

Li, M., Sun, Y., Lu, H., Maharjan, S., and Tian, Z. (2019). Deep reinforcement learning for partially observable information poisoning attack in crowdsensing systems. IEEE Intern. Things J. 7, 6266–6278. doi: 10.1109/JIOT.2019.2962914

CrossRef Full Text | Google Scholar

Lin, J., Yuan, Y., Shao, T., and Zhou, One thousand. (2020). "Towards high-fidelity 3D face up reconstruction from in-the-wild images using graph convolutional networks," in 2020 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 5891–5900. doi: 10.1109/CVPR42600.2020.00593

CrossRef Full Text | Google Scholar

Lu, Y., Yong, J. H., Shi, K. L., Song, H. C., and Ye, T. Y. (2016). 3D b-spline curve construction from orthogonal views with self-overlapping projection segments. Comput. Graph. 54, 18–27. doi: ten.1016/j.cag.2015.07.010

CrossRef Full Text | Google Scholar

Maejima, A., Kuratate, T., Pierce, B., Morishima, S., and Cheng, G. (2012). "Automatic face replacement for humanoid robot with 3D confront shaped display," in 2012 12th IEEE-RAS International Conference on Humanoid Robots (Osaka), 469–474. doi: 10.1109/HUMANOIDS.2012.6651561

CrossRef Full Text | Google Scholar

Meng, M., Lan, G., Yu, J., Wu, J., and Tao, D. (2020). Constrained discriminative project learning for paradigm classification. IEEE Trans. Image Procedure. 29, 186–198. doi: 10.1109/TIP.2019.2926774

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, M., Desbrun, M., Schroder, P., and Barr, A. H. (2003). Discrete Differential-Geometry Operators for Triangulated two-Manifolds. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-662-05105-4_2

CrossRef Full Text | Google Scholar

Mian, A., Bennamoun, M., and Owens, R. (2006). "Automatic 3D face up detection, normalization and recognition," in Third International Symposium on 3D Information Processing, Visualization, and Manual (3DPVT'06) (Chapel Hill, NC) 735–742. doi: 10.1109/3DPVT.2006.32

CrossRef Full Text | Google Scholar

Peng, W., Feng, Z., Xu, C., and Su, Y. (2017). "Parametric t-spline confront morphable model for detailed plumbing equipment in shape subspace," in IEEE Figurer Vision and Pattern Recognition (CVPR) (Honolulu, Hello), 5515–5523. doi: 10.1109/CVPR.2017.585

CrossRef Full Text | Google Scholar

Peng, West., Xu, C., and Feng, Z. (2016). 3D confront modeling based on structure optimization and surface reconstruction with b-spline. Neurocomputing 179, 228–237. doi: 10.1016/j.neucom.2015.xi.090

CrossRef Full Text | Google Scholar

Piotraschke, One thousand., and Blanz, V. (2016). "Automated 3D face reconstruction from multiple images using quality measures," in Proc. IEEE Computer Vision and Pattern Recognition (Las Vegas, NV), doi: 10.1109/CVPR.2016.372

CrossRef Full Text | Google Scholar

Prados, East., and Faugeras, O. (2005). "Shape from shading: a well-posed problem?," in IEEE Computer Vision and Pattern Recognition (CVPR), Vol. 2, (San Diego, CA), 870–877.

Google Scholar

Qiu, J., Tian, Z., Du, C., Zuo, Q., Su, S., and Fang, B. (2020). A survey on access control in the age of internet of things. IEEE Intern. Things J. 7, 4682–4696. doi: 10.1109/JIOT.2020.2969326

CrossRef Full Text | Google Scholar

Richardson, E., Sela, 1000., and Kimmel, R. (2016). "3D face reconstruction by learning from synthetic data," in International Conference on 3D Vision (3DV) (Stanford, CA), 460–469. doi: x.1109/3DV.2016.56

CrossRef Total Text | Google Scholar

Richardson, East., Sela, M., Or-El, R., and Kimmel, R. (2017). "Learning detailed face up reconstruction from a unmarried image," in IEEE Calculator Vision and Blueprint Recognition (CVPR) (Honolulu, HI), 5553–5562. doi: 10.1109/CVPR.2017.589

CrossRef Total Text | Google Scholar

Roth, J., Tong, Y., and Liu, X. (2016). "Adaptive 3D face up reconstruction from unconstrained photo collections," in Proc. IEEE Computer Vision and Blueprint Recognition. doi: 10.1109/CVPR.2016.455

PubMed Abstract | CrossRef Total Text | Google Scholar

Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and Szeliski, R. (2006). "A comparison and evaluation of multi-view stereo reconstruction algorithms," in 2006 IEEE Figurer Society Conference on Calculator Vision and Blueprint Recognition (CVPR'06) (New York, NY), 519–528.

Google Scholar

Sela, M., Richardson, E., and Kimmel, R. (2017). "Unrestricted facial geometry reconstruction using paradigm-to-epitome translation," in 2017 IEEE International Briefing on Computer Vision (ICCV) (Venice). doi: 10.1109/ICCV.2017.175

CrossRef Total Text | Google Scholar

Sengupta, S., Lichy, D., Kanazawa, A., Castillo, C. D., and Jacobs, D. Westward. (2020). SfSNet: Learning shape, reflectance and illuminance of faces in the wild. IEEE Trans. Pattern Anal. Mach. Intell. doi: 10.1109/TPAMI.2020.3046915

PubMed Abstract | CrossRef Total Text | Google Scholar

Shang, J., Shen, T., Li, S., Zhou, L., Zhen, M., Fang, T., et al. (2020). "Self-supervised monocular 3D face up reconstruction past occlusionaware multi-view geometry consistency," in Proceedings of the European Conference on Figurer Vision (ECCV) (Glasgow). doi: 10.1007/978-3-030-58555-6_4

CrossRef Full Text | Google Scholar

Sunday, Z.-L., Lam, One thousand.-M., and Gao, Q.-W. (2013). Depth estimation of face images using the nonlinear least-squares model. IEEE Trans. Prototype Process. 22, 17–30. doi: ten.1109/TIP.2012.2204269

PubMed Abstruse | CrossRef Full Text | Google Scholar

Tomasi, C., and Kanade, T. (1992). Shape and move from epitome streams under orthography: a factorization method. Int. J. Comput. Vis. 9, 137–154. doi: 10.1007/BF00129684

CrossRef Full Text | Google Scholar

Tran, A. T., Hassner, T., Masi, I., and Medioni, G. (2017). "Regressing robust and discriminative 3D morphable models with a very deep neural network," in IEEE Computer Vision and Pattern Recognition (CVPR), (Honolulu, HI). doi: 10.1109/CVPR.2017.163

CrossRef Full Text | Google Scholar

Wang, H., Wei, H., and Wang, Y. (2003). "Face representation under unlike illumination atmospheric condition," in International Conference on Multimedia and Expo (ICME) (Baltimore, Doc), 285–288.

Google Scholar

Wu, F., Bao, L., Chen, Y., Ling, Y., Song, Y., Li, South., et al. (2019). "MVF-net: multi-view 3D face morphable model regression," in IEEE Calculator Vision and Pattern Recognition (CVPR) (Long Beach, CA), 959–968. doi: 10.1109/CVPR.2019.00105

CrossRef Total Text | Google Scholar

Yang, C., Chen, J., Su, Northward., and Su, G. (2014). "Improving 3D face details based on normal map of hetero-source images," in IEEE Figurer Vision and Pattern Recognition Workshops (CVPRW) (Columbus, OH), nine–14. doi: ten.1109/CVPRW.2014.7

CrossRef Full Text | Google Scholar

Yuille, A. L., Snow, D., Epstein, R., and Belhumeur, P. N. (1999). Determining generative models of objects under varying illumination: shape and albedo from multiple images using SVD and integrability. Int. J. Comput. Vis. 35, 203–222. doi: 10.1023/A:1008180726317

CrossRef Full Text | Google Scholar

Zhang, L., Mistry, K., Jiang, M., Mentum Neoh, S., and Hossain, M. A. (2015). Adaptive facial point detection and emotion recognition for a humanoid robot. Comput. Vis. Image Understand. 140, 93–114. doi: 10.1016/j.cviu.2015.07.007

CrossRef Full Text | Google Scholar

Zhang, L., Snavely, N., Curless, B., and Seitz, S. M. (2017). "Spacetime faces: high-resolution capture for modeling and animation," in Information-Driven 3D Facial Animation eds Deng, Z., and Neumann, U. (Los Angeles, CA: Springer), 248–276. doi: 10.1007/978-1-84628-907-1_13

CrossRef Full Text | Google Scholar

Zhang, R., Tsai, P.-S., Cryer, J. East., and Shah, One thousand. (1999). Shape-from-shading: a survey. IEEE Trans. Pattern Anal. Mach. Intell. 21, 690–706. doi: 10.1109/34.784284

CrossRef Total Text | Google Scholar

Zhou, Y., Deng, J., Kotsia, I., and Zafeiriou, Southward. (2019). "Dense 3D face decoding over 2500 fps: joint texture shape convolutional mesh decoders," in IEEE Computer Vision and Pattern Recognition (CVPR) (Long Embankment, CA), 1097–1106. doi: 10.1109/CVPR.2019.00119

CrossRef Full Text | Google Scholar

Zhu, X., Lei, Z., Liu, X., Shi, H., and Li, Due south. Z. (2016). "Face up alignment beyond big poses: a 3D solution," in 2016 IEEE Briefing on Computer Vision and Pattern Recognition (CVPR), (Las Vegas, NV), 146–155. doi: 10.1109/CVPR.2016.23

CrossRef Full Text | Google Scholar

goinrobse1985.blogspot.com

Source: https://www.frontiersin.org/articles/10.3389/fnbot.2021.652562/full

Share this post